
 On étudie une population constituée de poissons et de requins.
On étudie une population constituée de poissons et de requins.
On étudie l’évolution des populations pour chaque espèce durant une succession de périodes.
Pour chaque période :
- 90% des poissons peuvent être mangés. Les 10% qui restent se cachent ;
- Chaque requin mange 2 poissons. S’il n’y a pas assez de poissons, les requins affamés meurent.
A la fin de chaque période, le nombre des requins augmente de 10% et celui des poissons de 20% (taux de renouvellement).
Le nombre maximal de poissons est 1 milliard.
Travail demandé :
- Suivre l’évolution du nombre d’individus de chaque espèce pendant 100 périodes.
Prendre par exemple 40 requins et 1 000 poissons ; 45 requins et 1 000 poissons.
- Modifier les paramètres comme le taux de renouvellement et observer les incidences.
| Niveaux |
Seconde à Terminale |
| Description générale du travail attendu |
Analyser les implémentations dans les divers langages ou écrire un algorithme, l’implémenter dans un langage.Observer, interpréter et faire une analyse critique d’une simulation. |
| Commentaires |
On peut montrer que la pérennité des espèces n’est jamais atteinte à long terme avec ce modèle :
Lorsque le nombre de poissons atteint Pmax=109, le nombre de requins augmente. Le nombre de poissons reste à Pmax, tant qu’il en reste Pmax/1,2 avant application du taux de renouvellement.
Pour ne pas voir leur population baisser, (Pmax-Pmax/1,2) poissons maximum doivent être mangés, ce qui correspond à (Pmax-Pmax/1.2)/2 requins (environ 83 millions pour Pmax=109). Lorsque ce nombre de requins est atteint, la disparition des deux espèces est inéluctable.
L’algorithme peut être modifié pour compter le nombre de périodes de pérennité. (Correction avec Algobox dans la liste des fichiers et exécutable Java (FPoissons.jar) avec graphiques) |
| Objectifs |
Algorithmique :
- Instructions élémentaires : affectation
- Boucle itérative (sans utilisation de l’itérateur)
- Boucle conditionnelle
- Instruction conditionnelle
Lien avec le reste du programme :
|
| Scénarios possibles |
- Les élèves analysent et modifient les programmes (en seconde) ;
- Les élèves complètent les programmes (en première) ;
- les élèves écrivent les programmes (en terminale).
On peut faire effectuer les calculs des premières étapes à la main pour amener à la pertinence de la mise en place d’une simulation informatique. |
| Téléchargement |
- Programme Algobox (voir en HTML/Javascript)
- Programme Python
[accordions id= »3863″]
[spoiler show= »Voir »]
- Programme Scilab [spoiler show= »Voir »]
[/spoiler]
- Programme PHP
[spoiler show= »Voir »]
<?php
/**
Pour chaque période, l'algorithme vérifie les règles suivantes :
- 90% des poissons peuvent être mangés. Les 10% restant se cachent.
- Chaque requin mange 2 poissons. S'il n'y a pas assez de poissons, les requins affamés meurent.
A la fin de chaque période, les requins augmentent leur nombre de 10% et les poissons de 20% (taux de renouvellement).
Le nombre maximal de poissons est 1 milliard.
*/
$requins = 40;
$poissons = 1000;
print("<strong>Simulation proie/prédateur</strong><br/>");
//100 périodes
for ($i=1 ; $i<=100 ; $i++) {
if (2*$requins < 0.9*$poissons) {
//Il y a assez de poisson. Tous les requins survivent
$poissons = $poissons-2*$requins;
}
else {
//Il manque de poisson. Il reste les 10% de poissons cachés et seuls les requins rassasiés survivent
$requins = floor(0.90*$poissons/2);
$poissons = floor(0.10*$poissons);
}
//On applique les taux de renouvellement
$requins = floor($requins*1.1);
$poissons = floor($poissons*1.2);
//Applique le nombre maximal de poissons
if ($poissons > 1000000000) $poissons = 1000000000;
//Affichage des données
echo("requins,poissons : ".$requins.",".$poissons."</br>n");
}
?>
- Programme C
[spoiler show= »Voir »]
- Programme Java [spoiler show= »Voir »]
[/spoiler]
Déterminer le nombre de périodes de pérennité :
|
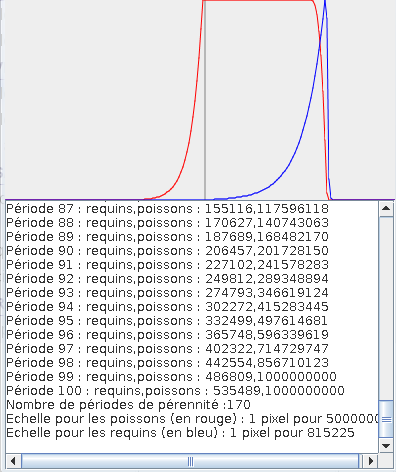

 On étudie une population constituée de poissons et de requins.
On étudie une population constituée de poissons et de requins.

