Par Gaëlle Chabod

Niveau : Terminale S

Objectifs :

• Comprendre et utiliser la méthode d’Euler ;
• Utiliser le tableur pour visualiser la courbe d’une fonction dont on ne connaît pas l’expression ;
• Mettre en évidence l’existence et l’unicité d’une primitive passant par un point ;
• Visualiser deux primitives d’une même fonction.

Place dans la progression : Cette activité peut être proposée après avoir traité la dérivation et introduit la notion de primitive..

Logiciel utilisés : Tableur

Prérequis :

• Dérivée d’une fonction ; approximation affine.
• Primitive d’une fonction.

Déroulement :

• Dans un premier temps, on compare les résultats obtenus par la méthode d’Euler avec les valeurs réelles de la fonction. Cela permet de « légitimer » la méthode, et également de constater que les approximations sont d’autant meilleures que le pas choisi est proche de 0 ;
• Dans un deuxième temps, on utilise la méthode d’Euler pour obtenir une représentation graphique approchée d’une primitive d’une fonction f. Cela permet de visualiser les résultats concernant les primitives d’une fonction continue … ;
• La troisième partie permet de visualiser l’existence d’une solution de l’équation différentielle y’=-2y² . L’utilisation des primitives permet de déterminer cette solution.

Remarque :
Cette activité est un peu longue … et les élèves qui ne sont pas à l’aise avec le tableur n’ont pas réussi à terminer … On peut donc proposer aux élèves de travailler sur la partie « présentation de la méthode », ainsi que sur les questions I a), b), c) (trouver les formules) à la maison …

 

Téléchargements :

• Fichier de consignes
  • format PDF
  • format DOC
  • format StarWriter SXW
• Fichier Tableur :
• format Excel XLS
• au format StarCalc SXC

[spoiler show= »Voir la présentation de la méthode »]

La méthode d’Euler

Présentation de la méthode …

Cette méthode est utilisée pour approcher la représentation graphique d’une fonction f  lorsqu’on connaît sa valeur en un réel x₀ et sa dérivée.
Le principe est basé sur l’approximation suivante :

pour h voisin de 0 : f(x+h)≈f(x)+h.f'(x)

En exploitant ce résultat, on peut approcher la courbe C de f à l’aide d’une courbe constituée de segments de droites.

On considère un réel h strictement positif.
On pose x₁ = x₀ + h ; x₂ = x₁ + h ; x₃ = x₂ + h ; ………………. ; x_n+1 = x_n + h .
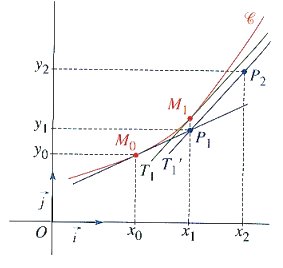
On considère les points M₀; M₁; M₂; ….. etc ….. de la courbe C, d’abscisse respective x₀; x₁; x₂; ……
Chaque point M_n a donc pour coordonnées (x_n ; f (x_n)).
On cherche à construire, uniquement à l’aide de la connaissance de f ‘ , une suite de points P₀; P₁; P₂ ; …., qui approchent les points M₀; M₁; M₂ ; …….. de la courbe C.
On part du point M₀ (x₀; f (x₀)) de la courbe C pour lequel f ‘(x₀) est non nul. On pose :

• y₁ = f (x₀) + h . f ‘ (x₀) et on construit le point P₁ (x₁ ; y₁)
  alors y₁≈ f (x₀ + h) c’est-à-dire y₁≈ f (x₁) donc le point P₁ est proche du point M₁.
• y₂ = y₁ + h . f ‘ (x₁) et on construit le point P₂ (x₂ ; y₂)

Comme y₁≈f (x₁) alors y₂ ≈f (x₁) + h . f ‘ (x₁)≈f (x₁ + h) = f (x₂) donc le point P₂ est proche du point M₂.

On recommence ainsi de suite …

On construit ansi une suite de points P_n (x_n ; y_n) tels que y_n+1 = y_n + h . f ‘ (x_n)

En joignant les points M₀ ; P₁ ; P₂ ; …….. on obtient une courbe affine par morceaux qui approche celle de f.

[/spoiler]

[spoiler show= »Voir l’étude d’un exemple avec le tableur »]

I Étude d’un exemple avec le tableur

On considère la fonction f définie sur l’intervalle [0 ; 4] par .
On souhaite observer la courbe obtenue par la méthode d’Euler, en comparaison avec la courbe de f.
a) Déterminer la fonction dérivée f ‘ de f .
b) On choisit ici x₀ = 0.    h étant un réel strictement positif fixé, la suite (x_n) est définie par x₀ = 0  et  x_n+1 = x_n + h
Définir ainsi la suite (y_n) obtenue par la méthode d’Euler pour cette fonction f .
Vous utiliserez la valeur de la dérivée trouvée pour expliciter clairement la valeur de y_n+1 en fonction de x_n
y₀ = ………       y_n+1 = ………………………………….
c) à l’aide d’un tableur, réaliser la feuille de calcul ci-dessous.

• On souhaite compléter ce tableau afin que tout soit recalculer automatiquement si l’on change la valeur du pas… Commencer par compléter la colonne A. (compléter A4 et A5, puis utiliser la poignée de recopie vers le bas.) S’arrêter lorsque l’on atteint la valeur 4 pour x_n.
  Quelle formule va-t-on écrire en B4, puis recopier vers le bas ?
  En C4, écrire  » = B4″. Quelle formule va-t-on écrire en C5, puis recopier ves le bas ?
  Compléter la colonne D par recopie d’une formule écrite en D4.
• Sélectionner la plage de cellules de A3:C24 et utiliser l’assistant graphique pour visualiser les courbes représentant f et son approximation par la méthode d’Euler.

d) Changer la valeur du pas hen mettant 0,1 dans la cellule B1. Qu’observez-vous sur le graphique ?
e) Recommencer en donnant à h la valeur 0,01.

II Utilisation de la méthode d’Euler pour approcher la courbe d’une primitive

Soit f  la fonction définie sur ]0;+∞[ par .

1) Justifier l’existence de primitives de f sur l’intervalle ]0;+∞[.

On considère F, primitive de f sur ]0;+∞[, vérifiant F(1) = 0.

2) En utilisant la méthode décrite précédemment, et en prenant 0,01 comme pas, on peut visualiser la courbe approximative de F sur [1 ; 4] .
Définir les suites (x_n) et (y_n) obtenues par la méthode d’Euler.
À l’aide du tableur, visualiser la courbe approximative de F obtenue.

On peut ainsi visualiser l’allure de F sans même connaître son expression ….

3) Soit G une autre primitive de f .On suppose dans un premier temps que G(1) = 5.

À l’aide du tableur et de la méthode d’Euler, représenter sur un même graphique les courbes approchées de F et de G sur l’intervalle [1 ; 4].
Modifier plusieurs fois la valeur de G(1). Que peut-on dire des courbes obtenues ?
Quel résultat visualise-t-on ainsi ?

4) Dans chacun des cas suivants, visualiser à l’aide de la méthode d’Euler la courbe représentative approchée de la primitive F de f vérifiant la condition initiale donnée.

a.  sur [0 ; 5] et F(0) = 1               b. f :  sur [0 ; 2] et F(0) = 0.

III Résolution d’une équation différentielle…

On cherche une fonction g dérivable sur [0 ; 1] et vérifiant g’ = -2 g² et .

1) En utilisant la méthode d’Euler, visualiser une approximation de la courbe de la fonction g.

 

2) Démontrer que g est décroissante sur [0 ; 1]. En déduire que g ne s’annule pas sur [0 ; 1], et que, pour tout réel x de l’intervalle [0 ; 1] on a .

3) Exprimer  en fonction de x et en déduire l’expression de g(x).

IV Complément : Construction approchée de la courbe d’une fonction exponentielle

1) On considère une fonction f définie sur IR et qui vérifie : f (0) = 1 et f ‘ = f.

a) Un pas h étant fixé, définir les suites (x_n) et (y_n) obtenues par la méthode d’Euler :

Pour la suite (x_n) : x₀ = …………. et x_n+1 = ……………………………………

Pour la suite (y_n) : y₀ = …………. et y_n+1 = ……………………………………………………………………

b) Utiliser le tableur pour visualiser la courbe approchée de f sur [0 ; 3]

On choisira dans un premier temps un pas égal à 0,2.

Modifier ensuite la valeur du pas : h = 0,1 et recommencer en prenant h = 0,01.

c) Donner à h la valeur – 0,1. Qu’obtient-on ?

La fonction définie sur IR, vérifiant f (0) = 1 et f ‘ = f , dont vous venez de construire une représentation graphique approchée, est appelée fonction exponentielle.

2) Équations différentielles du type y‘ = a y + b.

On considère une fonction g qui vérifie l’équation différentielle y‘ = 2y + 3 et vérifiant la condition initiale g (0) = 1

a) Un pas h étant fixé, définir les suites (x_n) et (y_n) obtenues par la méthode d’Euler :

Pour la suite (x_n) : x₀ = …………. et x_n+1 = ……………………………………

Pour la suite (y_n) : y₀ = …………. et y_n+1 = ……………………………………………………………………

b) Utiliser le tableur pour visualiser la courbe approchée de g sur [0 ; 2]. On choisira un pas égal à 0,01.

 

[/spoiler]