Une séance de Travaux Pratiques avec Géospace pour la classe de Seconde.
Par Daniel Muller

La géométrie dans le tétraèdre
Utilisation de Géospace (quelque soit la version)
- Un élève par poste. Géoplan a déjà été utilisé.
- Niveau : Classe de seconde.
- Objectif : Voir dans l’espace et réaliser un patron.
Annexe
Document papier que les élèves doivent compléter à télécharger au format pdf.
Télécharger :
Figures au format zip
Fiche élève au format doc
Étapes
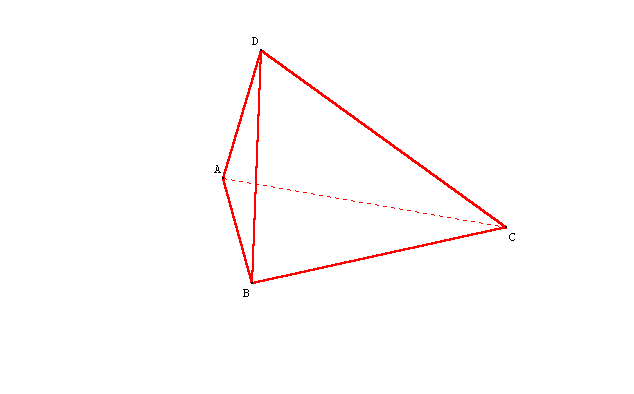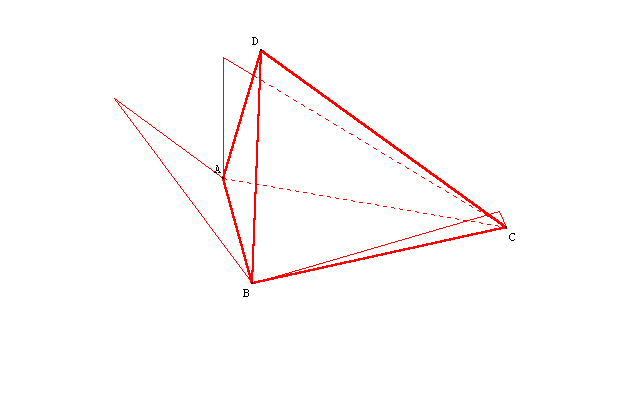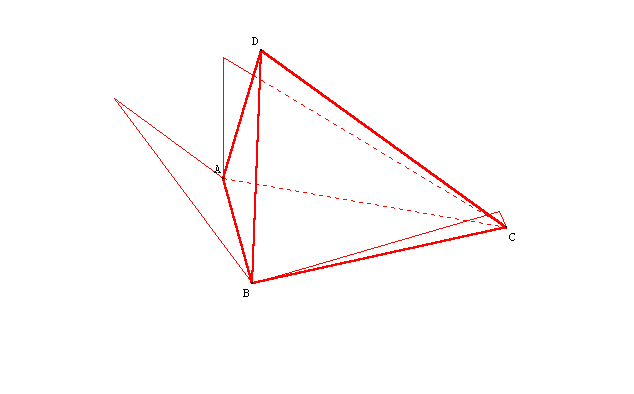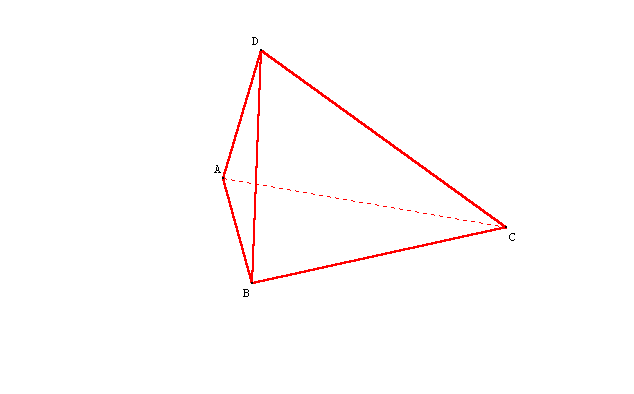
- Faire tourner la figure pour repérer la position d’un sommet devant ou derrière une face
- Construire le polyèdre des milieux et reconnaître la nature de ce polyèdre. L’élève pourra cacher le tétraèdre pour mieux isoler les parties essentielles à visualiser.
- Utiliser un tétraèdre dont les faces sont des triangles rectangles pour construire un patron.
La figure de base est mise à disposition des élèves par le réseau informatique.
figure Géospace élève
figure Géospace professeur

La mise en évidence des arêtes cachées est effectuée.
Les élèves apprennent à faire tourner la figure par des combinaisons de touches du clavier.
 |
 |
| Les segments des milieux sont tous marqués, certains sont cachés par le tétraèdre. | En masquant le tétraèdre ABCD tous les segments sont marqués en traits pleins. |
- Droites coplanaires : Par diverses rotations, on visualise les deux quadrilatères dans l’octaèdre.
- Le tableau à remplir précisera la position relative des droites portées par les segments.
- La visualisation en vraie grandeur permettra de guider la démonstration de la conjecture : « Les deux quadrilatères sont des parallélogrammes ».
Seconde étape
Le tétraèdre dont les faces sont des triangles rectangles.
Une seconde figure Géospace est mise à disposition par le réseau informatique. La construction par les élèves serait certainement trop longue, et ne présente pas d’intérêt majeur. Le paramètre numérique nécessaire à l’ouverture progressive du patron est déjà contenu dans la figure Géospace.
La figure Géospace
- Cette figure permettra d’effectuer des calculs en utilisant la relation de Pythagore dans différents plans de la figure.
- Le quadrillage proposé sur la fiche élève permet de réaliser le patron.


Le patron tel qu’il se présente en perspective

La vue en vraie grandeur pourra être demandée lors d’une évaluation. Cette vue est obtenue en se plaçant dans le plan ABC. Mais là, le patron n’est visible qu’une fois entièrement ouvert.