Par Bernard Lachambre
Le Problème
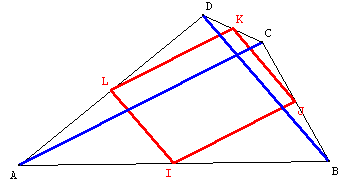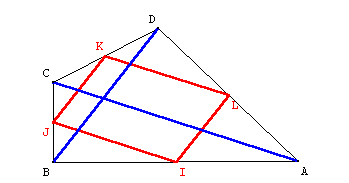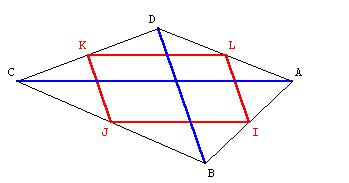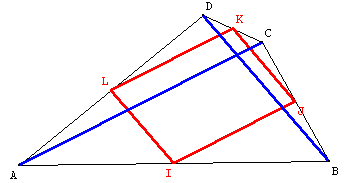
Un quadrilatère ABCD.
I, J, K, L les milieux de [AB], [BC], [CD], [DA].
Quelle est la nature du quadrilatère IJKL.
Ce problème peut être traité de la quatrième à la seconde. C’est une source de travaux intéressants.
On trouvera ci-dessous différentes pistes de travail que l’usage de l’outil informatique rend plus pertinentes.
Utilisation : un ordinateur en classe entière
Logiciel utilisé : GeoplanW
Pistes d’utilisations en classe
Lecture de la figure
Les élèves rencontrent souvent des difficultés à lire une figure. Il s’attachent à la situation particulière de leur figure ou de celle qui est dessinée au tableau. En conséquence, après avoir fait une figure personnelle, ils reprennent celle qui est faite au tableau.
L’usage de Géoplan peut d’abord aider à valider la construction de chacun en faisant varier la position des points A B C D. Il peut aussi obliger l’élève à travailler avec des situations différentes si la figure de travail affichée au tableau par Géoplan n’est pas toujours la même : il devra alors faire un travail d’association entre les éléments de sa figure et les éléments de celle du tableau. Ce travail peut l’aider à mieux voir les configurations présentes sur sa figure.
Aide à la démonstration
Trois pistes pour l’utilisation de la figure Géoplan :
- Isoler une configuration simple dans une figure complexe (Exemple ici : un triangle et une « droite des milieux »)
La commande déclenchée par l’appui sur la touche ‘0’ cache ou montre les éléments de la figure, des appuis répétés sur ‘0’ donne ceci :
Les élèves ont souvent des difficultés à extraire une configuration simple d’une figure complexe. Une telle animation peut contribuer à les y aider. - « Voir » un élément non dessiné (Exemple ici : imaginer, si elle n’est pas dessinée, une diagonale du quadrilatère ABCD)
La commande déclenchée par l’appui sur la touche ‘D’ cache ou montre la diagonale [AC], des appuis répétés sur ‘D’ donne ceci :
Les élèves n’osent pas ou ne pensent pas à construire des éléments non donnés dans l’énoncé. Mais l’observation fine de la figure peut donner une idée de configuration (incomplète) connue. Cette configuration apparaîtra sur une figure complétée. - Enchaîner les différentes étapes d’une démonstration (Exemple ici : (IJ)//(AC) et (KL)//(AC) donc (IJ)//(KL) )
L’appui successif sur les touches ‘1’, ‘2’, ‘3’, ‘4’ permet de donner un « film » de la démonstration.
Cas particuliers
Les figures réalisées par les élèves sont souvent des figures particulières, ce problème peut-être l’occasion suivant le niveau de la classe de travailler sur cette notion.
- Certaines figures particulières induisent une particularité pour le quadrilatère IJKL (ABCD rectangle ou losange), d’autres pas (ABCD trapèze ou parallélogramme)
- On arrive à des propriétés du type : « Si ABCD est rectangle alors IJKL est un losange ». Un travail sur la figure illustre que la réciproque est fausse. Mais par contre, on peut conjecturer « Pour que IJKL soit un losange il faut que ABCD ait des diagonales de même longueur »
Des commandes associées à la figure permettent d’obtenir instantanément des situations particulières, on peut aussi déplacer des points avec la souris.
Situations non classiques
Selon le niveau de la classe ou le niveau d’enseignement, on pourra explorer à l’aide de Géoplan des situations non classiques, par exemple : quadrilatères non convexes, quadrilatères croisés.
On pourra aussi chercher s’il est possible d’obtenir des parallélogrammes IJKL non classiques, par exemple : parallélogrammes aplatis, réduits à un segment, à un point (?), ayant une diagonale de longueur nulle.
Ces recherches peuvent être guidées par le professeur ou au contraire laissées à l’initiative des élèves. Dans ce cas, il peut être intéressant de réfléchir au concept de « cas particulier » et aux méthodes utilisées pour explorer une situation.
Téléchargement
[spoiler show= »Voir le texte de la figure Géoplan »]
Figure Géoplan
Numéro de version: 1Position de Roxy: Xmin: -4, Xmax: 1, Ymax: 2.8
Objet dessinable Roxy, particularités: rouge, non dessinéA point libre
Objet libre A, paramètres: -4.8, -1.5
B point libre
Objet libre B, paramètres: 2, -1.4
C point libre
Objet libre C, paramètres: 0.53, 1.2
D point libre
Objet libre D, paramètres: -0.74, 1.8
Segment [AB]
Segment [BC]
Segment [CD]
Segment [DA]
I milieu du segment [AB]
Objet dessinable I, particularités: rouge
J milieu du segment [BC]
Objet dessinable J, particularités: rouge
K milieu du segment [CD]
Objet dessinable K, particularités: rouge
L milieu du segment [DA]
Objet dessinable L, particularités: rouge
Segment [IJ]
Objet dessinable [IJ], particularités: rouge, trait épais
Segment [JK]
Objet dessinable [JK], particularités: rouge, trait épais
Segment [KL]
Objet dessinable [KL], particularités: rouge, trait épais
Segment [LI]
Objet dessinable [LI], particularités: rouge, trait épais
Segment [AC]
Objet dessinable [AC], particularités: bleu, trait épais, non dessiné
Segment [BD]
Objet dessinable [BD], particularités: bleu, trait épais, non dessinéCm0 (touche ESPACE) dessin en bloc de [BD], [AC]
Cm1 (touche D) dessin en bloc de [AC]
Cm3 (touche 1) dessin en bloc de [JK], [KL], [LI], [DA], [CD], K, L, D, [AC]
Cm4 (touche 2) dessin en bloc de [AB], [BC], [IJ], J, I, B, [DA], [CD], [KL], K, L, D
Cm5 (touche 3) dessin en bloc de [AB], [BC], B, I, J, [IJ]
Cm6 (touche 4) dessin en bloc de [JK], [LI], [AC]
Cm7 (touche V) position mémorisée de A, B, C, D
Paramètres pour Cm7: -4.8671269356 -1.5 2 -1.42 0.5285 1.265 -1.78 1.676
Cm8 (touche W) position mémorisée de A, B, C, D
Paramètres pour Cm8: -4.8540381249 -1.424 2 -1.421 2 1.663 -4.854 1.66
Cm9 (touche X) position mémorisée de A, B, C, D
Paramètres pour Cm9: -4.854 -1.424 -0.674 -1.424 2.057 1.752 -2.148 1.752
Cm10 (touche Y) position mémorisée de A, B, C, D
Paramètres pour Cm10: -3.28 -0.738 -0.674 -1.424 2.057 1.752 -2.148 1.752
Cm11 (touche Z) position mémorisée de A, B, C, D
Paramètres pour Cm11: -4.854 -1.424 2 -1.42 1.98 0.609 -3.621 2.48
Cm2 (touche 0) dessin en bloc de D, L, K, [KL], [JK], [LI], [BD], [DA], [CD]Commentaire
Usage des commandes :
ESPACE : montre les 2 dialonales.
D montre la diagonale [AC].
Tapez successivement 1 2 3 4 pour voir une animation sur la démonstration
(il faut auparavant que les diagonales ne soient pas visibles.
V W X Y Z : positions particulières.
[/spoiler]
(Des commentaires rappelant le fonctionnement de la figure peuvent être affichées, dans Géoplan, avec la touche F3)